Fork me on GitHub

BZOJ4663 Hack

发表于 | | 阅读次数:
字数统计: 836

传送门

%%%Newuser，直接秒掉了

一句话题意：割掉一些边使得S，T之间不连通且S->T的路径上仅有一条割边

考试题

首先看题面和数据范围，就可以知道跟最小割有关。

普通的最小割可以实现前一半，那么如何处理后一半呢？

先放一张样例

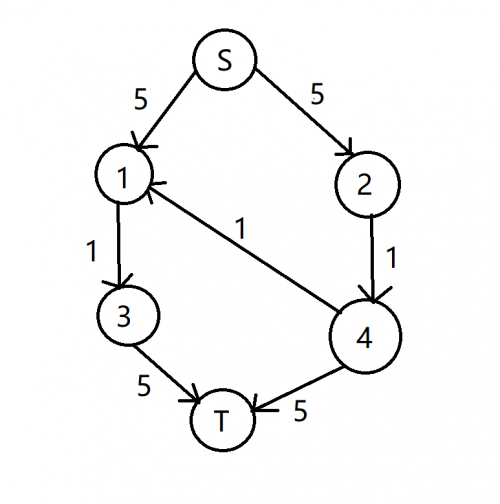
直接跑最小割答案是2，即切掉1->3,2->4

但我们发现，那S->2->4->1->3->T这条路径上就有两条割边了

那么想让这种情况不成立，即使得这个割不是个割==>使得S，T连通

我们可以连一条1->4的边使得S，T联通

为了防止这条边被割，我们把这条边的容量变为inf即可

那么我们可以给每条边连一条反向的容量为inf的边

因为最小割是所有正向割边的权值和，所以就算加边时加入了反向边，这种边被割了也不会对答案造成影响。

由于容量为inf，所以只会在其他方案都不成立时割这条边，那么答案若大于inf就输出-1

你以为完了？？？

再来看这个图

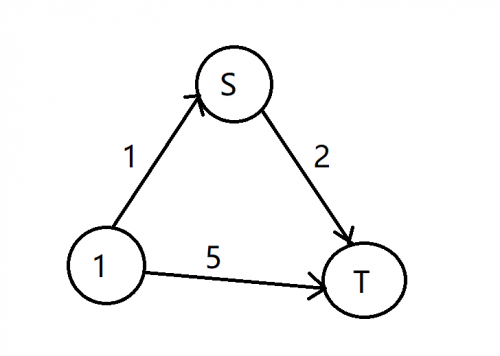
显然答案为2，只要割掉S->T就行了

但用上面的方法跑出来是7

为什么？

仔细一想，反向边虽然不影响答案，但会使得有些一开始不存在的S->T的路径存在，如S->1->T

那么一开始先把图连好，把S不能到的点标记了，再往网络流里加边。

因为到不了，所以跟到不了的点连的边自然也不用加入网络流了

于是你就A掉了此题

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include<stdio.h>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector> 
#define inf 0x3f3f3f3f3f3fll
#define ll long long
#define maxn 10005
using namespace std;
int N,M;
int S,T;
int Last[maxn],Next[maxn],End[maxn],o=1;
int U[maxn],V[maxn];
ll W[maxn];
vector<int>G[maxn];
bool mark[maxn];
ll Len[maxn];
ll dis[maxn];
int cnt[maxn];
void ins(int a,int b,ll c){
	Next[++o]=Last[a],Last[a]=o;
	End[o]=b,Len[o]=c;
}
void inss(int a,int b,ll c){
	ins(a,b,c),ins(b,a,0);
}
ll sap(int u,ll flow){
	if(u==T||!flow)return flow;
	ll sum=0,tmp;
	for(int i=Last[u],v;i;i=Next[i]){
		v=End[i];
		if(Len[i]&&dis[u]==dis[v]+1){
			tmp=sap(v,min(Len[i],flow-sum));
			Len[i]-=tmp,Len[i^1]+=tmp;
			sum+=tmp;
			if(sum==flow||dis[S]>=T)return sum;
		}
	}
	if(dis[S]>=T)return sum;
	cnt[dis[u]]--;
	if(!cnt[dis[u]])dis[S]=T;
	dis[u]++;
	cnt[dis[u]]++;
	return sum;
}
bool vis[maxn];
void dfs(int u){
	vis[u]=1;
	for(int i=0,v;i<G[u].size();++i){
		v=G[u][i];
		if(!vis[v])dfs(v);
	}
}
int main(){
	scanf("%d%d",&N,&M);
	S=1,T=N;
	for(int i=1;i<=M;++i){
		scanf("%d%d%lld",&U[i],&V[i],&W[i]);
		U[i]++,V[i]++;
		G[U[i]].push_back(V[i]);
	}
	dfs(S);
	for(int i=1;i<=M;++i){
		if(!vis[U[i]]||!vis[V[i]])continue;
		inss(U[i],V[i],W[i]);
		inss(V[i],U[i],inf);
	}
	ll ret=0;
	while(dis[S]<T){
		ret+=sap(S,inf);
		if(ret>=inf){
			printf("-1");
			return 0;
		}
	}
	printf("%lld",ret);
	return 0;
}
0%
``` ```